Hoeveel aardbevingen gebeuren er gemiddeld per jaar?
Het aantal aardbevingen groter dan een bepaalde magnitude (kracht op de schaal van Richter) daalt logaritmisch met de magnitude, volgens de zgn. relatie van Gutenberg-Richter:
$$\log(N) = a - b \cdot M$$Waarbij:
- N: jaarlijks aantal aardbevingen met magnitude groter dan M
- M: magnitude
- a, b: constanten
Meestal is b ongeveer gelijk aan 1, wat betekent dat aardbevingen groter dan een bepaalde magnitude tienmaal minder frequent voorkomen dan aardbevingen van één magnitude-eenheid lager.
Het wereldwijd jaarlijks gemiddelde voor verschillende magnitude-intervallen werd berekend door de USGS:
| Magnitude | Aantal aardbevingen |
|---|---|
| ≥ 8 | 1 |
| 7-7.9 | 17 |
| 6-6.9 | 134 |
| 5-5.9 | 1319 |
Voor België en grensgebieden kan op basis van de aardbevingscatalogus van de Koninklijke Sterrenwacht van België de volgende relatie berekend worden:
$$\log(N) = 2.84 - 0.89 \cdot M$$Het verband wordt verduidelijkt door de volgende grafiek:
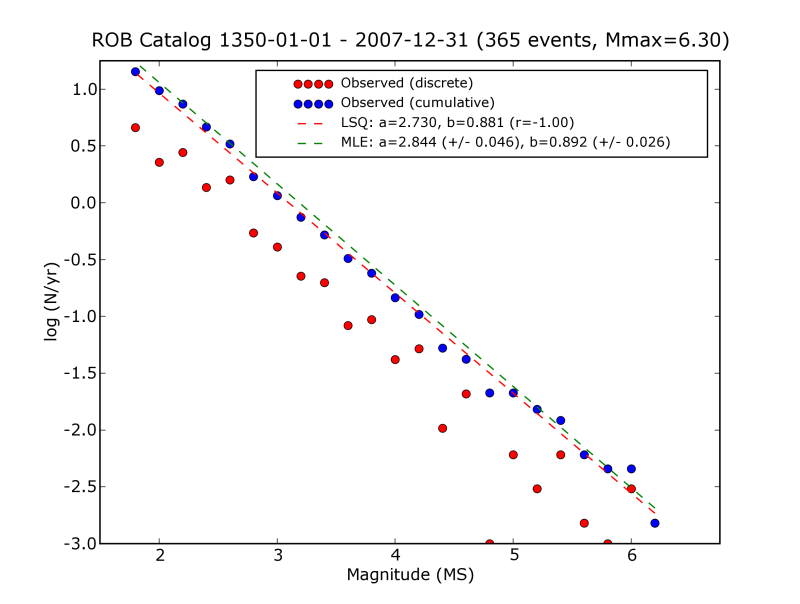
Het gemiddeld aantal aardbevingen dat jaarlijks geregistreerd wordt bedraagt aldus:
| Magnitude | Aantal aardbevingen |
|---|---|
| ≥ 6 | 1 om de 315 jaar |
| ≥ 5 | 1 om de 40 jaar |
| ≥ 4 | 1 om de 5 jaar |
| ≥ 3 | 1.5 per jaar |
| ≥ 2 | 11 per jaar |
